Legfrissebb híreink
- Valós felhasználói élményre hangolva – indul a 4K streaming teszt
- Az ASUS Republic of Gamers lett a 2026-os PGL szezon hivatalos monitor-, PC- és perifériapartnere
- Megérkeztek a Club 3D idei első újdonságai
- HONOR Magic8 Pro: az AI, amely előre gondolkodik helyetted
- Tűzfalak és VPN-ek élmezőnyében: újabb rangos elismerést kapott a Zyxel
Hol számíthatunk a pontosabb helymeghatározást biztosító EGNOS korrekciókra?
 Az EGNOS műholdak láthatósága az álláspont, a domborzati viszonyok és a beépítettség függvényében
Az EGNOS műholdak láthatósága az álláspont, a domborzati viszonyok és a beépítettség függvényében
Bár a valóban megbízható EGNOS korrekciók vételére még várnunk kell, édemes megvizsgálni azt, hogy egyáltalán hol számíthatunk rájuk.
Bevezetés
A GPS és a majdani Galileo rendszerekhez kapcsolódó muhold alapú kiegészíto rendszerek szolgáltatásai közül Európában és Magyarországon ingyenes elérhetosége és a vétel egyszerusége miatt a geostacionárius (tehát mindig a Föld egy adott pontja felett található) holdakról sugárzott EGNOS korrekciók állnak az érdeklodés középpontjában. Sajnos a technikai problémákkal küszködo, még mindig nem teljesen kiépített rendszer - különösen itthon, a szolgáltatási terület szélén - továbbra sem teljesíti a kituzött rendelkezésre állási, integritási és pontossági szintet, így a megbízható EGNOS korrekcók vételére egyelore várnunk kell.
Addig is érdemes azonban megvizsgálnunk, hogy mit várhatunk az EGNOS-tól álláspontunk és a domborzati viszonyok függvényében! Az interneten keresztül elérheto, illetve valamilyen földi rádiófrekvenciás megoldással sugárzott korrekcióktól most eltekintünk, és csak a muholdakról érkezo EGNOS jelek vételi lehetoségeit vizsgáljuk, hiszen egyelore ez jelenti a tömeges alkalmazást. Utóbbi esetben a vevo és a muhold között összelátás szükséges, ami a földrajzi helyzetünk, illetve a tereptárgyak vagy a domborzat kitakarása miatt sok esetben sajnos nem biztosítható.
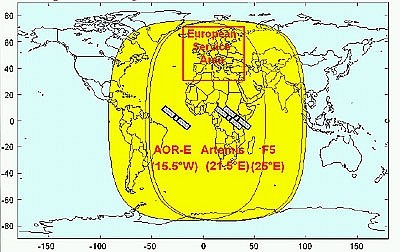
A sárga foltok a muholdak elméleti szolgáltatási területét, a piros négyzet az EGNOS hozzávetoleges európai lefedettségét jelöli. A muholdak alatt zárójelben azok meridiánja szerepel. (Forrás: ESA)
Jelenleg három, az Egyenlíto felett mintegy 35 000 km-es magasságban elhelyezkedo geostacionárius muholdról sugároznak EGNOS korrekciókat (1. ábra), amelyek a teszfázis miatt eltéro tartalmúak. Az ESA ARTEMIS muholdja (PRN 124) és az Indiai-óceán feletti egyik Inmarsat-hold (IOR-W, PRN 126, az 1. ábrán F5-tel jelölve) már a kezdeti muködés (EGNOS Initial Operations) jeleit sugározza, míg az Atlanti-óceán feletti AOR-E Inmarsat-muhold (PRN120) még a kísérleti fázisban (EGNOS System Test Bed) kialakított rendszer szerint adja a korrekciókat.
A muholdak geostacionáriusak, tehát hozzávetolegesen a Föld egy adott pontja felett találhatóak, ám a pályán több kilométeres nagyságrendu elmozdulások történnek, így koordinátáik is ilyen mértékben változnak az idoben. Mivel ezek a holdak 30-40 000 km-re vannak Európától, ezek a mozgások a felszíni pontból számított szöghelyzetben (azimutban és magassági szögben) elhanyagolható mértéku változást jelentenek. A láthatósági vizsgálatokba mindhárom muholdat bevontam. Az AOR-E és az IOR-W muholdak pozíciójaként elore megadott XYZ térbeli derékszögu koordinátákat vettem. Az ARTEMIS-hez nem találtam hasonló adatot, így a nominális pályamagassággal (35 853 km), mint ellipszoid feletti magassággal, valamint fi = 0°, lambda = 21,5° fölrajzi szélesség- és hosszúságértékekkel számoltam.
Az alábbiakban három szinten vizsgálom a muhold és a vevo közötti geometriai viszonyokat. Eloször azt számoltam ki, hogy Európa területén hogyan változik pontról-pontra az egyes muholdak magassági szöge, azaz az álláspontunk horizontja és a muhold iránya között a függoleges síkban bezárt szög. Második lépésben egy norvégiai, egy erdélyi és egy magyarországi mintaterületre olyan térképeket készítettem, amelyen elkülönülnek azok a területek, ahol az egyes muholdak a domborzat miatt takarásban vannak. Végül helyi szintre érkezve a beépített környezetben jelentkezo kitakarásokat vizsgáltam a budapesti belváros egy részletére.
1. Az EGNOS muholdak láthatósága Európában
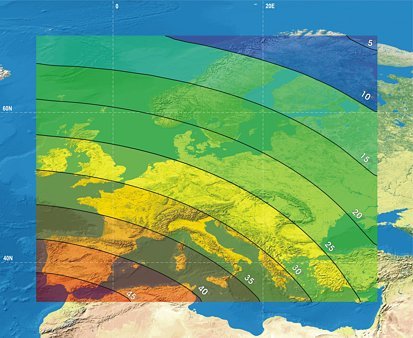
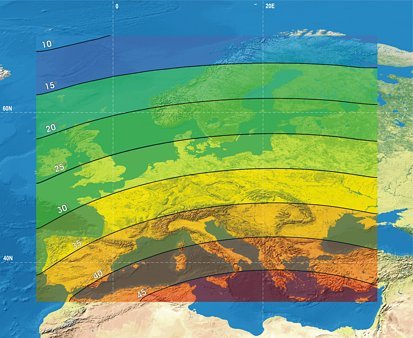
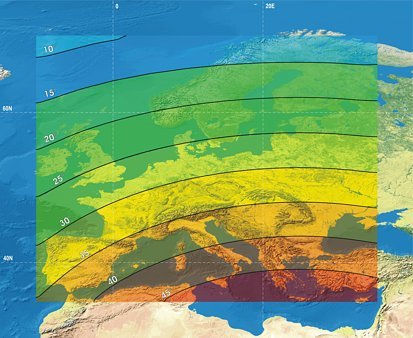
Egy Európát jórészt lefedo, a 70°É, 35°É, -10°Ny és 35°K ívek által határolt területre a domborzat és a tereptárgyak figyelmebevétele nélkül, állandó, 150 méteres ellipszoid feletti magasságra vonatkozóan elkészítettem az egyes muholdak magassági szögének izovonalas térképét.
Az izovonalak eloállítására olyan módszert választottam, hogy a mintaterület öt fokonkénti rácspontjaiban, összesen 80 pontban kiszámítottam az adott muholdra mutató vektor magassági szögét, melyeket a rácsháló pontjaihoz rendelt z-értékekként értelmeztem. Ezután krigeléssel létrehoztam egy surített rácsot, majd abból, mint domborzatmodellbol szintvonalakat, azaz 5 fokonkénti izovonalakat vezettem le.
A magassági szögek számításakor eloször az álláspont WGS84 ellipszoidi (fi , lambda) földrajzi koordinátáiról áttértem térbeli derékszögu koordinátákra. (Ugyanezt az ARTEMIS muhold esetében is meg kellett tenni, a másik két holdnál viszont eleve XYZ koordináták voltak adottak.) Ezután koordináta-különbségeket képeztem, melyet egy R forgatási mátrixszal szorozva megkaptam a muholdnak az álláspontra, mint topocentrumra vonatkozó topocentrikus koordinátáit, melybol az azimutra mutató vektor hossza és az azimut mellett kiszámoltam a magassági szöget.
A fentieket muholdanként megismételtem a mintaterület 80 rácspontjára, amelybol 80-80 koordinátahármas állt elo. A pontokból krigeléssel egy 78 x 100 pontosra surített rácshálót hoztam létre. Hogy bizonyos szögértékeket izovonalas formában is meg lehessen jeleníteni, a fenti rácshálóból, mint domborzatmodellbol egy 5 egységenként vett szintvonalas fedvényt készítettem, ahol a szintvonalközök diszkrét magassági színezést kaptak. Végül az alábbi képeket úgy állítottam elo, hogy az izovonalas térképet kombináltam egy távérzékelési adatokból szerkesztett, georeferált raszteres fedvénnyel. (Megjegyzem, hogy a fenti számítások nem veszik figyelembe a troposzféra és az ionoszféra hatását a hullámterjedés irányára.)
Az ábrák alapján is nyilvánvaló, hogy Európa egésze szempontjából az ARTEMIS muhold elhelyezése a legkedvezobb, az IOR-W láthatósága pedig alig rosszabb ennél.
2. A muholdak láthatósága a domborzat függvényében
A domborzat kitakaró hatásának számításához olyan szoftvereket használtam, amelyek képesek egy domborzatmodell minden egyes cellájára kiszámítani, hogy egy adott ponton elhelyezett objektum látszik-e onnan, vagy sem. A kipróbált eljárások a Föld görbületének figyelembevételével készítenek láthatósági térképeket. A funkciót eredetileg földi telepítésu adótornyok tervezésére szánták. Esetünkben a nagy távolság miatt az algoritmus és a számítógép kapacitása sajnos nem engedte meg a geostacionárius muholdak eredeti helyzetére vonatkozó láthatósági számítások elvégzését.
Jóval kisebb muhold-felszín távolságra viszont elvégezheto a láthatósági vizsgálat a fenti szoftverekkel, amely közelíto eredményként azért elfogadható. Ezért a muhold azimutjának és magassági szögének megtartása mellett, a muhold-vevo vektor hosszának csökkentésével "eltoltam" a muholdat, és erre a földközeli pozícióra számítottam láthatóságot.
Az eltolás számításához egy olyan képletsorozatot állítottam össze, amely a megfigyelo álláspontja és a valódi muholdhelyzet koordinátáiból indul ki, de egy tetszoleges méretarány-tényezovel csökkentheto a muhold-vevo vektorhossz, amelybol eloállnak az eltolt muholdkoordináták XYZ térbeli derékszögu, illetve ebbol számított ellipszoidi földrajzi koordinátákkal.
Az alábbiakban bemutatott térképek készítésekor álláspontnak a célterület középpontját vettem, a hegyvidéki jelleg miatt 300 méteres (Erdélyben 500 méteres) magassággal. A méretarány-tényezo megválasztásakor sajnos további kompromisszumokat kellett kötni: amennyire lehetett, igyekeztem távolra venni a muholdakat, de végül az alkalmazás - a felhasznált domborzatmodell és a magassági szög függvényében - csak 79 és 7,6 km közötti vektorhosszakra tudta a láthatósági térképet elkészíteni. Ilyen feltételek mellett a magassági szög kis területen is jelentosen változik. Minél közelebb helyezzük a muholdat, annál kisebb területre ad jó közelítést a számítás.
Mindig a leheto legnagyobb muhold-vevo távolságra számított térképeket közlöm, az álláspont környezetét tartalmazó kivágataban. Sajnos még ezek a kivágatok is valamennyire torzítottak az EGNOS holdakra nézve, így a valódi és a különféle távolságokkal számolt kitakart foltok nagysága, alakja eltéro lehet, ám elhelyezkedés és arány tekintetében talán az alábbi térképek is jó közelítést adnak. Megjegyzem, hogy a láthatóság-számításnál a szoftver (mikrohullámú sugárzásra vonatkozó) atmoszférikus korrekciót is alkalmaz, ám ennek elhagyásával csak alig észreveheto mértékben változik a végeredmény.
Az elso mintaterület Dél-Norvégiában van a 60. szélességi kör alatt valamivel, egy erosen tagolt, fjordos vidéken. 3 fokmásodperces cellaméretu (90-60 m) SRTM domborzatmodellt használtam, és csak az ARTEMIS muholdra számoltam láthatóságot (5. ábra). 1/500-ad részére csökkentettem a muhold-vevo vektor hosszát, amely így közel 79 km hosszúságú volt.
A második mintaterület Erdélyben a Gyergyói-havasokban, a Békás-szoros környékén található. A láthatósági vizsgálatot Az AOR-E és az ARTEMIS muholdakra végeztem el, utóbbihoz hasonló képet adna az IOR-W vizsgálata. 1/1000-ed részre csökkentett, 38 ill. 39 km-es muhold-vevo vektorhosszakkal történt a számítás, melynek eredménye a 6. ábrán látható. Az eleve kisebb magassági szögön felül az AOR-E láthatóságát a muholdnak a hegység csapására meroleges azimutja is kedvezotlenül befolyásolja.
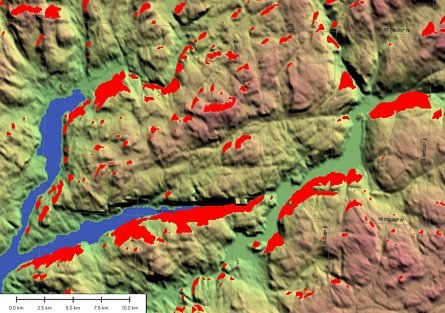
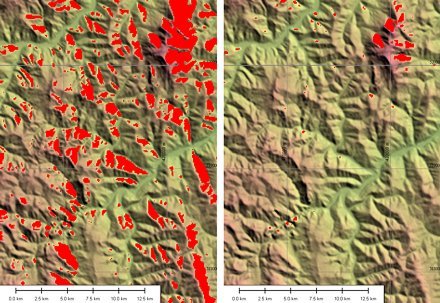
6. ábra. Balra az AOR-E, jobbra az ARTEMIS muhold láthatósága az erdélyi mintaterületen, SRTM domborzati adatokkal. A piros területeken a muhold a domborzat takarásában van. A képek bal alsó részeire esik a Gyilkos-tó, jobb fölso sarkokban pedig a Csalhó tömbje látható.
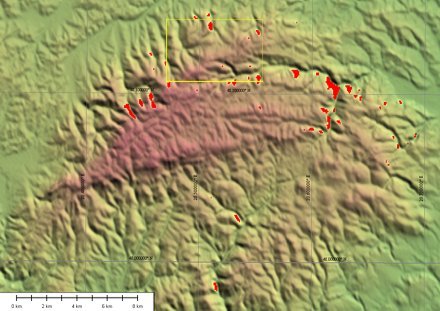
Harmadikként hazai mintaterületnek a Bükk hegységet választottam, mivel az elozetes próbálkozások során a leginkább kitakaró hegységek egyike volt. Eloször SRTM domborzatmodellen végeztem el a számítást az ARTEMIS és az AOR-E muholdakra. Az 1/1000-ed részére csökkentett muhold-vevo vektorok hossza 38 és 39 kilométer lett. Az áthelyezett ARTEMIS hold a Bél-ko lejtojét kivéve a modell minden pontjáról láthatónak adódott (7. ábra), míg az AOR-E (9. ábra) több kis foltban került takarásba.
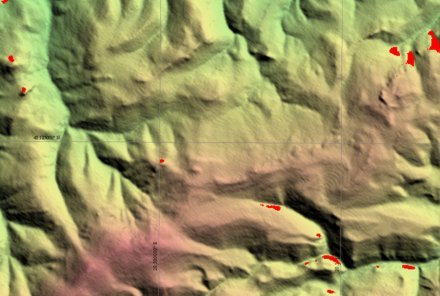
Mivel az SRTM domborzatmodell túl elnagyolt és simított ahhhoz, hogy huen kövesse a szuk völgyek talpát, ezért a Bükkön belül, Miskolc-Ómassa körzetében bevontam a vizsgálatba egy 11 méteres rácssuruségu, részletesebb, és jóval pontosabb domborzatmodellt, amelyet az 1:10 000 méretarányú EOTR topográfiai térkép 5 méteres alapszintközzel szerkesztett szintvonalrajzából generáltam. A muhold-vektor hosszakat 1/5000-ed részére csökkentettem, így az 7,6 és 7,8 km-re rövidült. Amint az várható volt, az ARTEMIS (8. ábra) és AOR-E (10. ábra) muholdakra készített láthatósági térképeken az utóbbi domborzatmodellen már több kitakart terület jelent meg.
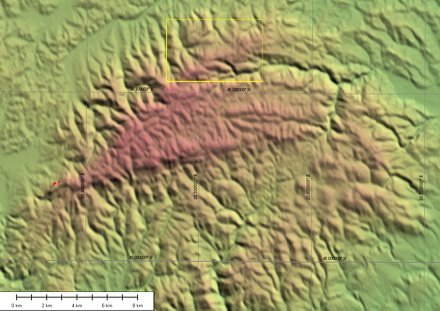
7. ábra. Az (áthelyezett) ARTEMIS muhold láthatósága a Bükkben, SRTM domborzati adatokkal. A piros területeken a muhold a domborzat takarásában van. A 7. ábra helyét a sárga keret mutatja.
Összefoglalva elmondható, hogy csak nagyon pontos domborzatmodellel, és kis területre vonatkozóan lehet a fenti módszerrel megbízhatóan láthatóságot számolni. Gyakorlati szempontból fontos megjegyezni, hogy a valóságban a nem épített környezet részérol további akadályozó tényezot jelent a növényzet.
3. Az EGNOS muholdak láthatósága beépített területen
Az épített környezet kitakaró hatását Budapest belvárosában, a Duna - Kossuth Lajos utca - Múzeum körút - Vámház körút által határolt területen vizsgáltam. Alapanyagként rendelkezésemre állt egy 3D vektoros háztömbmodell Microstation DGN formátumban, EOV rendszerben, amely a BME Fotogrammetria és Térinformatika Tanszékén készült a 2000. évi országos légifényképezésbol származó sztereopárok fotogrammetriai kiértékelésével (11. ábra).

A láthatósági vizsgálathoz használt szoftver képes a domborzatmodellen elhelyezett, magassági attribútummal rendelkezo vektoros elemek kitakaró hatásának figyelembevételére. A kapott állományt nem tudtam közvetlenül beolvasni, és egy utca kimaradása miatt amúgy is javítani kellett volna a modellen, így újra rajzoltam azt. A bevitel az eredeti 3D tömbök síkvetülete alapján történt, figyelembe véve az 1:10 000 méretarányú EOTR topográfiai térkép tömbhatárait is. Az egyes háztömbök tetejének tengerszint feletti magasságát a DGN állomány alapján adtam meg. Az utcák szintjének egy állandó, 108 m-es magasságú "domborzatmodellt" alkalmaztam, ahogyan az a 3D modellben is szerepelt.
A kitakarás által érintett területek kiszámítását az elozo fejezetben említett módon, a muholdak irány- és magassági szögének megtartása mellett, azok közelebb hozásával végeztem el az ARTEMIS (12. ábra) és az AOR-E (13. ábra) muholdakra.
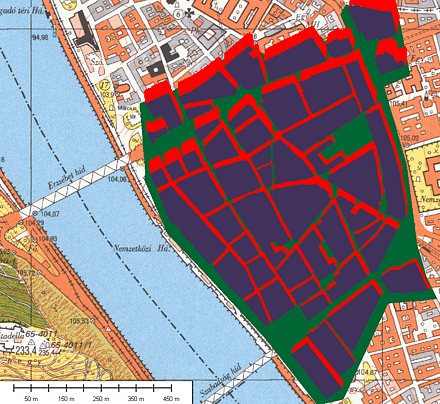
12. ábra. Az ARTEMIS muhold láthatósága a budapesti belváros egy részletén. Az összelátással rendelkezo közterületeket zöld színnel, a kék színnel jelölt épületek miatt takarásban lévoket pedig pirossal jelöltem.
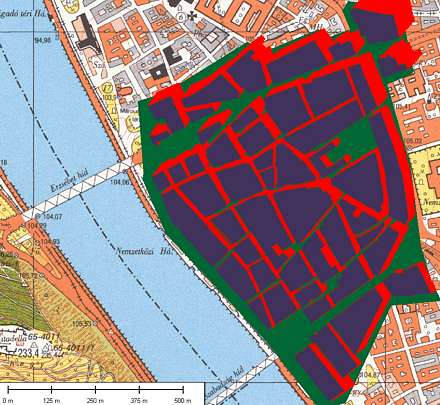
13. ábra. Az AOR-E muhold láthatósága a budapesti belváros egy részletén. Az összelátással rendelkezo közterületeket zöld színnel, a kék színnel jelölt épületek által kitakart részeket pedig pirossal jelöltem.
Ezúttal 1/20 000-ed részére, vagyis durván két kilométeresre kellett csökkenteni a muhold-vevo távolságot: így volt képes elvégezni a program a láthatósági számítást 2 méteres rácssuruséggel. Az áthelyezéssel az AOR-E hold látszólag nagyjából a Feneketlen-tó mellé, az ARTEMIS pedig az Irinyi József utcában a 4-es és a 6-os villamosok elágazása fölé került, 1350 ill. 1600 méteres magasságba. Ez a közelíto módszer a terület középpontjától, mint referencia ponttól a muhold felé haladva a valósnál nagyobb magassági szöget (kedvezobb láthatóságot) ad, míg távolodva a valódinál kedvezotlenebb képet rajzol a kisebb látszólagos magassági szögek miatt. A láthatóságot nem az utca szintjére, hanem annál egy méterrel magasabbra számoltam, amely megfelel az általános autós vagy gyalogos használatnak.
Az eredmények a várakozásoknak megfeleloen azt mutatják, hogy ilyen beépítettség mellett az EGNOS jelek vételére a mellékutcákban szinte egyáltalán nem, a foutakon pedig csak alkalomszeruen nyílik lehetoség. Ezen a képen az sem változtat számottevoen, ha figyelembe vesszük a muhold közelebb hozásával okozott eltéréseket.
Kapcsolódó oldal: